Page 23 - ITUJournal Future and evolving technologies Volume 2 (2021), Issue 1

ITU Journal on Future and Evolving Technologies, Volume 2 (2021), Issue 1

0.5
more time to converge.
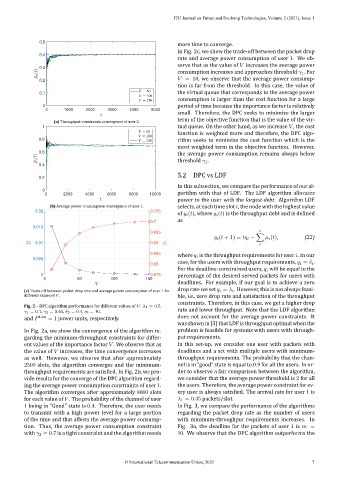
In Fig. 2c, we show the trade‑off between the packet drop
0.4
rate and average power consumption of user 1. We ob‑
serve that as the value of V increases the average power
0.3
consumption increases and approaches threshold γ 1 . For
V = 10, we observe that the average power consump‑
0.2
tion is far from the threshold. In this case, the value of
0.1 the virtual queue that corresponds to the average power
consumption is larger than the cost function for a large
0 period of time because the importance factor is relatively
0 1000 2000 3000 4000 5000
small. Therefore, the DPC seeks to minimize the larger
term of the objective function that is the value of the vir‑
(a) Throughput‑constraints convergence of user 2.
1 tual queue. On the other hand, as we increase V , the cost
function is weighted more and therefore, the DPC algo‑
0.8 rithm seeks to minimize the cost function which is the
most weighted term in the objective function. However,
0.6 the average power consumption remains always below
threshold γ 1 .
0.4
5.2 DPC vs LDF
0.2
In this subsection, we compare the performance of our al‑
0
0 2000 4000 6000 8000 10000 gorithm with that of LDF. The LDF algorithm allocates
power to the user with the largest‑debt. Algorithm LDF
(b) Average power consumption convergence of user 1. selects, at each time slot t, the node with the highest value
0.02 0.705
of y i (t), where y i (t) is the throughput debt and is de ined
as
0.7
0.015
t
0.695 ∑
y i (t + 1) = tq i − µ i (t), (22)
0.01 0.69
τ
0.685 where q i is the throughput requirements for user i. In our
0.005
0.68 case, for the users with throughput requirements, q i = δ i .
For the deadline‑constrained users, q i will be equal to the
0 0.675 percentage of the desired served packets for users with
0 50 100 150
deadlines. For example, if our goal is to achieve a zero
drop rate we set q i = λ i . However, this is not always feasi‑
(c) Trade‑off between packet drop rate and average power consumption of user 1 for
different values of V . ble, i.e., zero drop rate and satisfaction of the throughput
constraints. Therefore, in this case, we get a higher drop
Fig. 2 – DPC algorithm performance for different values of V . λ 1 = 0.5,
γ 1 = 0.7, γ 2 = 0.65, δ 2 = 0.4, m = 10. rate and lower throughput. Note that the LDF algorithm
and P Low = 1 power units, respectively. does not account for the average power constraints. It
was shown in [3] that LDF is throughput optimal when the
In Fig. 2a, we show the convergence of the algorithm re‑ problem is feasible for systems with users with through‑
garding the minimum‑throughput constraints for differ‑ put requirements.
ent values of the importance factor V . We observe that as In this set‑up, we consider one user with packets with
the value of V increases, the time convergence increases deadlines and a set with multiple users with minimum‑
as well. However, we observe that after approximately throughput requirements. The probability that the chan‑
2500 slots, the algorithm converges and the minimum‑ nel is in “good” state is equal to 0.9 for all the users. In or‑
throughput requirements are satis ied. In Fig. 2b, we pro‑ der to observe a fair comparison between the algorithm,
vide results for the converge of the DPC algorithm regard‑ we consider that the average power threshold is 2 for all
ing the average power consumption constraints of user 1. the users. Therefore, the average power constraint for ev‑
The algorithm converges after approximately 8000 slots ery user is always satis ied. The arrival rate for user 1 is
for each value of V . The probability of the channel of user λ 1 = 0.35 packets/slot.
1 being in “Good” state is 0.4. Therefore, the user needs In Fig. 3, we compare the performance of the algorithms
to transmit with a high power level for a large portion regarding the packet drop rate as the number of users
of the time and that affects the average power consump‑ with minimum‑throughput requirements increases. In
tion. Thus, the average power consumption constraint Fig. 3a, the deadline for the packets of user 1 is m =
with γ 2 = 0.7 is a tight constraint and the algorithm needs 10. We observe that the DPC algorithm outperforms the

© International Telecommunication Union, 2021 7